Pentagram

Pentagram

Pentagram si coby symbol života, zdraví a lásky, za své tajné poznávací znamení zvolili pythagorejci, vyznavači pythagoreismu, což je filosofická esoterní škola s významnou tradicí západního myšlení. Tato škola vychází z úvah o významu čísel. Bylo by však chybou se domnívat, že všechno toto vzešlo až z předsókratovské doby filosofa Pythagora. Učení je ve skutečnosti mnohem starší a jeho "prapočátek" můžeme umístit minimálně až do doby Starého Egypta, kde se však vyučovalo pouze pro vyvolené. Učení bylo tajné a nesmělo se předávat veřejnosti. Tím, že toto nařízení bylo postupem času porušováno, jeví se nám, jako by bylo nově objeveno právě ve Starém Řecku.

Učení o pentagramu máme úzce spojené s planetou Venuší.

Pentagram narýsovaný pomocí kružnic.

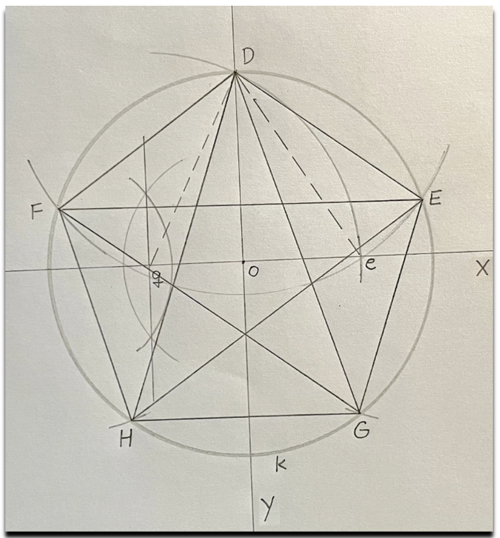
Postup:
1. narýsujte si kříž (osy x a y) a získáte bod o
2. vytvořte kružnici k (zde poloměr 5 cm)
3. pomocí průniku dvou kružnic (vytvořením Vesici Piscis) najděte bod g, střed poloměru kružnice na ose x
4. vezměte do kružítka vzdálenost od bodu g do bodu D a narýsujte část kružnice s protnutím na ose x, získáte bod e
5. vezměte do kružítka vzdálenost od bodu D do bodu e a narýsujte kružnici, která protne základní kružnici k a to na dvou místech a získáte tak body E a F
6. ponechte si vzdálenost v kružítku a z bodu E narýsujte protnutí na kružnici k a získáte bod G
7. a se stejnou vzdáleností v kružítku, avšak z bodu F získáte bod H
8. spojte body D, E, F, G a H, získáte pentagon
9. spojením špiček pentagonu získáte pentagram

Narýsování pentagramu pomocí vesici piscis.

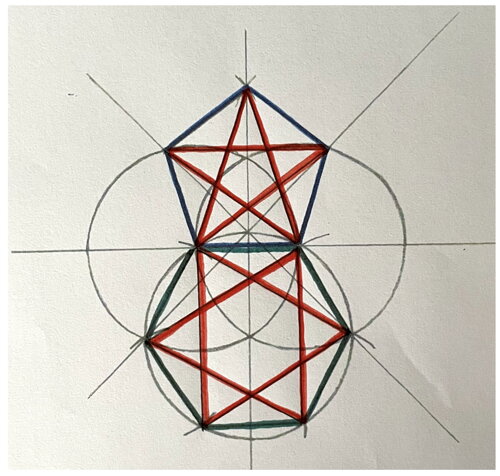
Postup:
1. narýsujte kružnice k1, k2 a k3 se stejným poloměrem. Kružnice k1 má střed v bodě a, kružnice k2 má střed v bodě b a kružnice k3 má střed v bodě c.
2. narýsujte přímky p1 a p2, přímka p1 prochází body a a b, přímka p2 prochází body c a d.
3. důležitý bod o vznikne na kružnici k3 a přímce p2. Bodem o veďte další přímky. Přímka p3 vede přes bod e a bod o a vytvoří na kružnici k2 bod f. Přímka p4 vede přes bod g a bod o a vytvoří na kružnici k1 bod h.
4. bod i vznikne na přímce p2 pomocí kružnic ze středů h a f poloměrem mezi body f a b (h a a).
5. spojením bodů a - h - i - f - b vznikne pentagon a uvnitř pentagonu pentagram.

Pentagram a hexagram propojení skrze vesicu piscis.
Avšak, nejedná se o přesné propojení, protože strana pentagonu není ve skutečnosti naprosto stejná jako strana hexagonu. Je o něco větší.

Rychlejším způsobem je nakreslení pentagramu ne jenom přes vesicu piscis, ale přímo přes triquetru.

Zlaté řezy v pentagramu

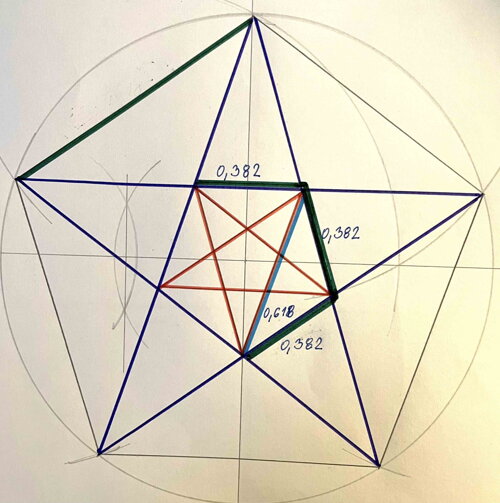
Narýsování pentagramu pomocí triquetry

„Triquetra neboli také trikvetra (z latinského tri – tři, a quetrus – opatřený rohem, původně prostě ve významu trojúhelník) je mytologický symbol mnoha významů. Původně toto označení znamenalo téměř jakýkoliv třírohý symbol, dnes se označení většinou používá pro složitější geometrické útvary, z nichž nejtypičtější je zobrazen vpravo. Trikvetra obecně většinou znamená neoddělitelné spojení tří prvků, může mít ale jiný význam.

V keltském umění, kde je často spojován s dalšími symboly (kde měla význam nejrůznějších trojic z keltského chápání světa, např. narození – život – smrt, tělo – mysl – duše, země – moře – nebe apod.). Dva symboly jsou doloženy na germánských runových kamenech a mincích, kde symbolizoval především tzv. valknut, symbol nejasného významu spojovaný s bohem Ódinem přezdívaný jako „uzel padlých".

Symbol byl rozšířen i v křesťanském umění, kde symbolizoval Svatou Trojici, byl také interpretován jako „ztrojení" dávného křesťanského symbolu, stylizované ryby."

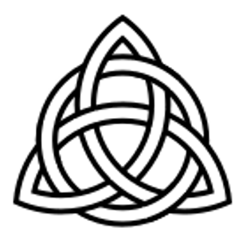
Zdroj: https://cs.wikipedia.org/wiki/Triquetra

Rýsování triquetry

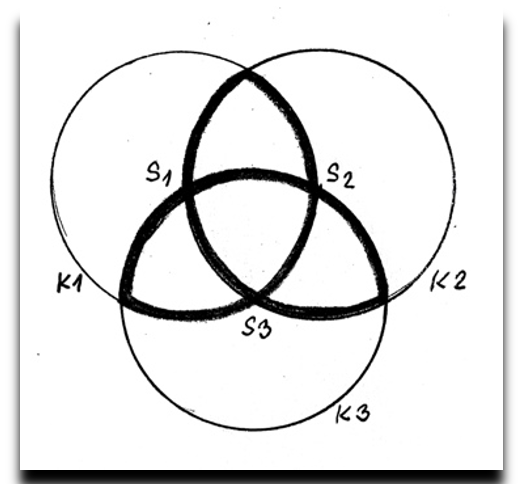
Kružnice k1, k2 a k3 ze středů s1, s2 a s3.
V podstatě z kružnice 1 a kružnice 2 dostaneme vesicu piscis.
Přidáme-li kružnici 3 získáme triquetru.

Postup rýsování pentagramu pomocí triquetry je stejný jako u vesici piscis, ale my si v tomto případě všímáme, že onu triquetru tam ve skutečnosti také rýsujeme.

Opět se držíme na zcela nečekaném místě v podstatě nauky o Tao.

„Tao rodí jedno,
jedno rodí dva,
dva rodí tři
a tři rodí všechny bytosti."

My tedy ze dvou – vesici piscis – získáme tři – triquetru.

Co vyjadřuje triquetra?
Rovnostranný trojúhelník

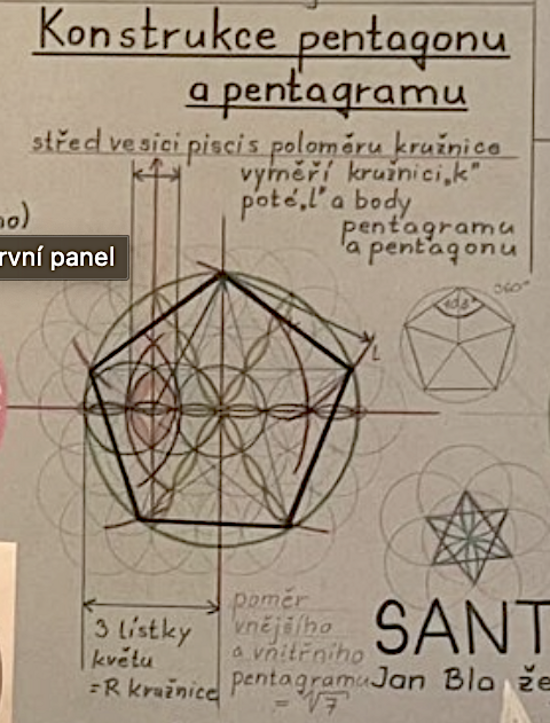
Známý a používaný způsob rýsování pentagramu pomocí kružítka má původ v Květu života.

Běžné rýsování pentagramu začíná v polovině poloměru kružnice. Když rýsování provádíte v Květu života, zjistíte, že ona polovina poloměru kružnice je přesně ve středu vesici piscis (oranžová) tvořené dvěma překrývajícími se kruhy (světle modrá).

V poloměru kružnice (vodorovně) se nachází přesně tři vesici piscis.

Světle zeleně zvýrazněné tři linie lístků právě v tomto natočení Květu života odkazují na zlatokorunskou rozetu (růžová rozeta níže). Toto natočení rozety tedy odkazuje na konstrukci pentagramu, který se v ní šest krát nachází.

Světle tyrkysově je vyznačený hexagram, přesně takový se nachází i v rozetě.

Rozeta - kruhové okno. Cisterciácký klášter Zlatá Koruna (původní název Svatá Trnová Koruna). Tento klášter založil český král Přemysl Otakar II., jako svůj jediný cisterciácký klášter. Lokaci kláštera provedl Hirzo z Klingenberku, který byl jistý čas i purkrabím na Zvíkově.

Všechna čísla velikosti jednotlivých úhlů v pentagramu, pentagonu, ale také z pentagramu vycházející hvězdě Síria můžeme prostým numerologickým součtem sečíst na nejmenší možné číslo od 1 do 9.

Příklady:

• 108° - 1 + 0 + 8 = 9
• 36° = 3 + 6 = 9
• 72° = 7 + 2 = 9

Výsledkem je, že vždycky při sčítání všech jednotlivých úhlů získáme číslo 9.

Tím pádem máme posvátný pentagam spojený s božským číslem 9.

Nákres s dalšími úhly, které je opět možné numerologickým součtem zjednodušit až na číslo 9.

V nákresu je navíc označený původ motivu draka, tedy přesněji papírového draka, kterého na podzim pouštíme s dětmi. Jeho rozměry opět vychází z pentagramu.