Molekula C60
Jak to vypadá, když Indiana Jones potká Santiniho na vlakovém nádraží?
Exkluzivní obsah a nové články najdete na HeroHero (Tania, Alchymistka-Tania's Secret) .
Obsah zdarma je umístěný také na YouTube - Alchymistka - Tania's Secret
Facebooková stránka: Tania's Secret: Papoušek mezi světy

Molekula C60 patří mezi fullereny, což jsou molekuly, které jsou tvořené atomy uhlíku uspořádanými do vrstvy složené z pětiúhelníků a šestiúhelníků.
Atomy jsou umístěné na vrcholech těchto mnohoúhelníků.
Fulleren je prostorově svinutý, nejčastěji do tvaru koule nebo elipsoidu (prostorový ovál). Díky této struktuře je mimořádně odolný vůči vnějším fyzikálním vlivům.
Teoreticky předpověděl existenci uhlíkových klastrů a některých jejich vlastností japonský chemik Eiji Osawa v 70. letech.
Za objev a studium vlastností fullerenů byla v roce 1996 udělena Nobelova cena za chemii Robertu F. Curlovi, Richardu E. Smalleymu a Haroldu W. Krotovi.
Objevitelé pojmenovali tento fulleren Buckminsterfullerenem po americkém architektovi Buckminster Fullerovi, který je autorem mnoha geodetických kopulí, podobných vzhledem molekule C60. Zemřel v roce 1983, rok před objevem fullerenu.
Molekulu C60 tvoří:
- 20 x šestiúhelník (hexagon)
- 12 x pětiúhelník (pentagon)
A právě propojení pentagonů a hexagonů nás velice zajímá, neboť matematicky není přesné. Ovšem, můžeme-li se volně vyjádřit, mohli bychom říci, že vesmíru je to úplně jedno (že to nesedí) a stvořil molekulu C60.
Propojení pentagonů (pentagramů) a hexagonů (hexagramů) skrze vesicu piscis a triquetru v molekule C60 je ukazatelem na další záhadu zlatokorunské rozety.
Rozeta je kruhové okno v gotické architektuře, a ve Zlaté Koruně se nachází jeho velice výjimečná podoba. Tato rozeta kdysi dávno nebyla veřejnosti vůbec přístupná. Více o Zlaté Koruně najdete zde. O Zlaté Koruně jsem také napsala knihu - Tajemný klášter pod horou.

Kde se v rozetě nachází molekula C60?
Připomeňme si, že molekulu C60 tvoří:
- 20 x šestiúhelník (hexagon)
- 12 x pětiúhelník (pentagon)
Šestiúhelníky
20 x šestiúhelník v molekule C60, kde je v rozetě?
Kolem každého pentagonu (pětiokvětního květu po obvodu kruhu) se nachází tři trojúhelníky (trojúhelníkovité listy).
Pentagonů je v rozetě celkem šest.
6 x 3 = 18 trojúhelníků
Ještě potřebujeme dva trojúhelníky, ty najdeme přímo v samotném středu rozety v podobě hexagonu (a ten se skládá ze dvou protilehlých trojúhelníků).
6 x 3 = 18 + 2 = 20
Dobře, ale to máme trojúhelníky, nikoliv šestiúhelníky (hexagony). Co tedy s tímto výpočtem provést?
Násobíme dvěma.
Tento početní úkon nám naznačují zdvojené hlavní listy v rozetě.
6 x 3 = 18 + 2 = 20 x 2 = 40 trojúhelníků
A 40 proti sobě otočených trojúhelníků (tento způsob propojení nám jasně ukazuje prostřední hexagram) vytvoří 20 šestiúhelníků (hexagonů).
Pětiúhelníky
Potřebujeme 12 pentagonů.
Správnost výpočtu u šestiúhelníků ověříme shodným postupem u pětiúhelníků (pentagonů).
V rozetě se nachází šest pětiúhelníků (pětiokvětních květů, pentagonů), opět vynásobíme dvěma (ukazatelem výpočtu jsou zdvojené listy v rozetě. Ty samy o sobě ukazují na číslo 6 x 2 = 12).
6 pětiúhelníků x 2 = 12 pětiúhelníků
Pětiúhelníky jsou v rozetě tvořeny přímo sebou samými a nijak se neskládají z jiných tvarů.
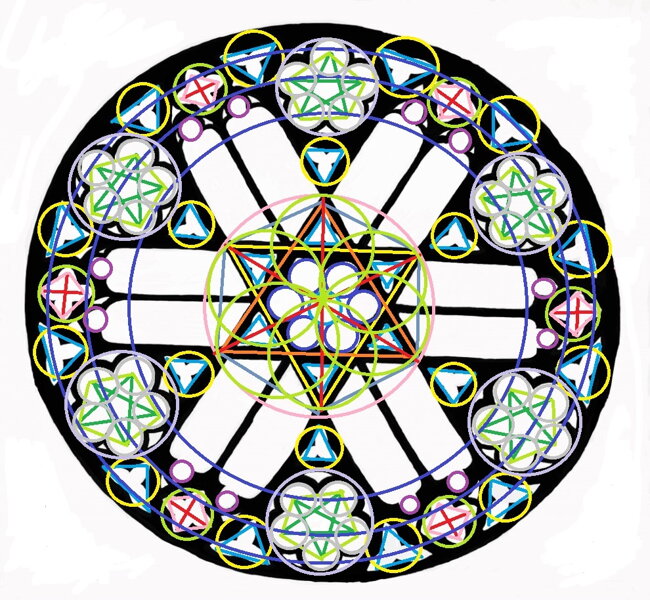
Rozeta a molekula C60
Ve zlatokorunské rozetě se tedy opravdu schovává molekula C60 tvořená 20 hexagony a 12 pentagony, které je možné propojit skrze vesicu piscis a triquetru a vytvořit kouli.
Ale jak je to možné?
Archimédovské těleso
Jedná se v geometrii o tělesa vysoce symetrická, polopravidelné konvexní mnohostěny, které jsou složené ze dvou nebo více typů pravidelných mnohoúhelníků setkávajících se v identických vrcholech.
Platónská tělesa se naproti tomu skládají pouze z jednoho typu mnohoúhelníků. Také se setkávají v identických vrcholech.
Archimédes o těchto tělesech psal ve svých spisech, proto jsou pojmenována po něm.
V období renesance byly objeveny nové formy těchto těles.
Molekula C60 = Archimédovské těleso komolý dvacetistěn:
- 20 šestiúhelníků (hexagonů)
- 12 pětiúhelníků (pentagonů)

Zdroj obrázku: Wikipedia
Archimédovská tělesa například zde.
Zajímavost o uhlíku
- grafit je tvořen v šesterečné struktuře - tedy v systému rovnostranných trojúhelníků
- diamant je tvořen v krychlové struktuře - tedy v systému rovnoramenných trojúhelníků
Rovnoramenný a rovnostranný trojúhelník získáme v triquetře.




